When to use the z-test versus t-test

How do I know when to use the t-test instead of the z-test?

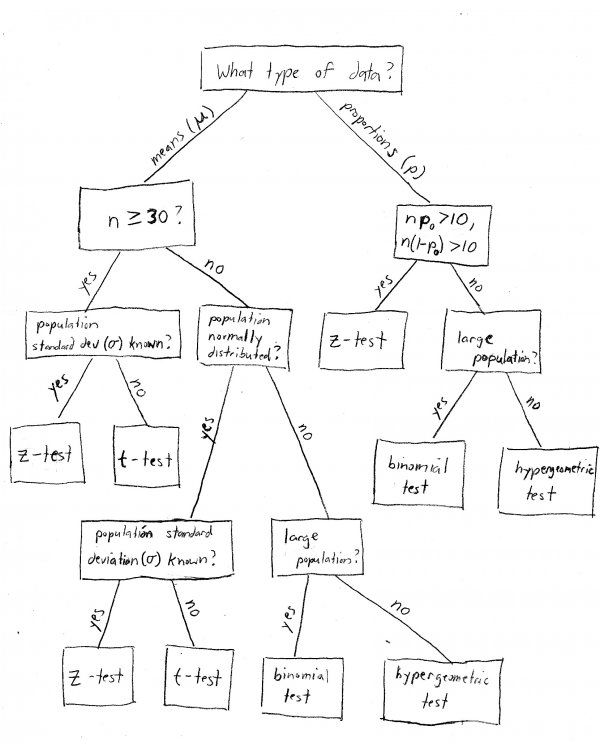
Just about every statistics student I've ever tutored has asked me this question at some point. When I first started tutoring I'd explain that it depends on the problem, and start rambling on about the central limit theorem until their eyes glazed over. Then I realized, it's easier to understand if I just make a flowchart. So, here it is!

Basically, it depends on four things:

1. Whether we are working with a mean (for example, "37 students") or a proportion (e.g., "15% of all students").
2. Whether or not we know the population standard deviation (\(\sigma\)). In real life we usually don't, but statistics courses like to contrive problems where we do.
3. Whether or not the population is normally distributed. This is mainly important when dealing with small sample sizes.
4. The size of our sample. The magic number is usually 30 - below that is considered a "small" sample, and 30 or above is considered "large". When the sample size is large, the central limit theorem tells us that we don't need to worry about whether or not the population is normally distributed.

When you're working on a statistics word problem, these are the things you need to look for. Proportion problems are never t-test problems - always use z! However, you need to check that \(np_{0}\) and \(n(1-p_{0})\) are both greater than 10, where \(n\) is your sample size and \(p_{0}\) is your hypothesized population proportion. This is basically saying that the population proportions (for example, % male and % female) should both be large enough so they will be adequately represented in the sample.

Generally speaking, the problem will explicitly tell you if the population standard deviation is known - if they don't say, assume that it's unknown. The same goes for a normally distributed population - if they don't say "assume the population is normally distributed", or something to that effect, then do not just make up that assumption. Fortunately if the sample size is large enough, it doesn't matter!

Get started with a statistics tutor at IU today!