M119 Notes - Week 2 - Supply and Demand

1.4b Budget constraint problem with fixed prices for 2 items

You have a budget of 500 dollars for books (\(x\)) and CDs (\(y\)). The total spent on books is \(55x\) and the total spent on CDs is \(15y\). Write an equation in the form of \(y = mx+b\) then solve for \(y\).

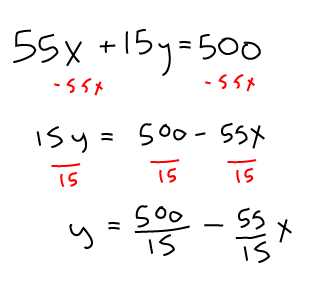
Supply and demand problems

Supply and demand both relate quantity \(q\) of an item to the price \(p\).

Supply curve: Increasing function. \(q\) increases as \(p\) increases

• The higher the price that sellers can charge for an item, the more quantity they will produce.
• If sellers can NOT sell an item for more money than it costs to manufacture, then they would choose not to manufacture it.

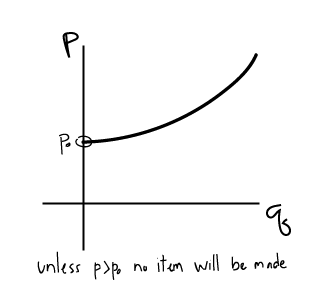
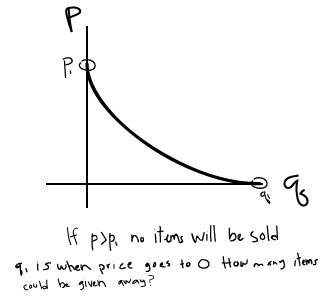
Demand Curve: Decreasing function. \(q\) decreases as \(p\) increases

• The more an item costs, the less buyers will want to buy it (less quantity will be demanded).
• If price is too high, NO items will be sold.

Equilibrium point: It is assumed that the market settles to an equilibrium point when \(S(p) = D(p)\).

• The supply and demand curves intersect.
• Corresponds to a specific price and quantity.

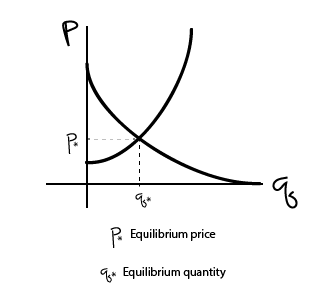
EXAMPLE

Find the equilibrium \(p\) and \(q\) for the following supply and demand functions:
\(S(p) = 10p - 500\)
\(D(p) = 2500 - 20p\)

1. Set \(S(p)\) equal to \(D(p)\).
   
   \(10p - 500 = 2500 - 20p\)
   
2. Solve for \(p\).
   
   \(30p = 3000\)
   \(p = 100\)
   
3. To solve for \(q\), notice the \(S(p)\) or the supply at any given price is actually \(q\) or the quantity.
   
   \(q = S(p) = 10p - 500\)
   
4. Plug in the value that you got for \(p\) into that equation.
   
   \(q = 10*100 - 500\)
   \(q= 500\)
   

Taxes

• Two kinds:
  • Tax on consumers: sales tax, affects demand curve.
  • Tax on producers: affects supply curve.
• How taxes affect supply and demand curves:
  • For a tax of \(x\) dollars, supply curve is \(S(p-x)\).
  • For a tax of \(x\) dollars, demand curve is \(D(p+x)\).
  • For a tax of \(x\%\), supply curve is \(S(p-px)\).
  • For a tax of \(x\%\), demand curve is \(D(p+px)\).
• Taxes will affect equilibrium.

How do taxes affect suppliers and producers?

The price of an item was 100 dollars and a tax of 6 dollars is imposed. The price is now 102 dollars. How much tax is paid by the consumer? How much is paid by the producers?